What Is the Reference Angle of 7Pi Over 4? Decoding the Trigonometric Benchmark

At first glance, 7π/4 appears as a fraction基準点 seemingly abstract, but within the sphere of trigonometry, it represents a precise 225-degree angle measured counterclockwise from the positive x-axis—a critical reference angle vital to simplifying complex periodic functions. Converting this angle into standard position reveals why the 45-degree standard reference angle dominates exercises in trigonometry: 7π/4 radians equals 315 degrees in degrees, placing it in Quadrant IV, where cosine and sine values alternate opposite in sign. Understanding this reference angle unlocks clarity across calculus, physics, and engineering applications.

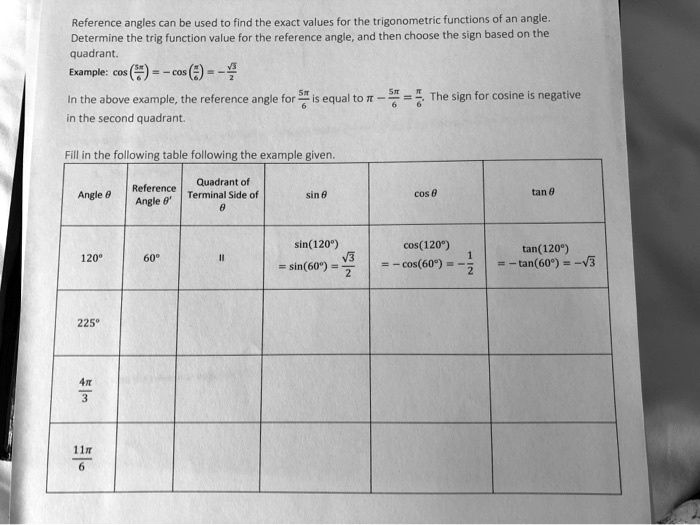
The reference angle is defined as the smallest positive acute or obtuse angle between the terminal side of a given angle and the nearest x-axis. For angles measured in radians or degrees, it strips away quadrant complexity by yielding a universally applicable baseline for evaluating trigonometric functions. In the case of 7π/4, its position at 315 degrees cuts cleanly across Quadrant IV—a region where cosine remains positive but sine is negative.

This symmetry allows direct use of the reference angle 45° (or π/4 radians), enabling efficient computation across multiple trigonometric functions.

Precision in Angle Conversion: From Radians to Reference Angles

Converting 7π/4 radians to degrees requires multiplying by 180/π: (7π/4) × (180/π) = (7 × 180) / 4 = 1260 / 4 = 315 degrees. This value confirms the angle lies 45 degrees east of the negative x-axis—precisely the standard location defining its reference angle. Since 7π/4 exceeds π radians (180°) but falls before 3π/2 (270°) + 45°, it settles squarely in Quadrant IV.

In this region, the reference angle is computed as: Reference angle = 2π − θ, or in degrees: 360° − θ. Thus, 360° − 315° = 45°, establishing that the reference angle of 7π/4 is 45°—or π/4 radians—mirroring the foundational symmetry of the unit circle.

Why does this reference angle matter so profoundly?

Trigonometric functions harbor periodicity and symmetry: sine and cosine, for example, retain identical magnitude but opposite signs across quadrants based on their reference angle and quadrant location. By anchoring calculations to π/4—the simplest unit circle angle with well-known sine and cosine values (√2/2 and √2/2)—mathematicians avoid redundant computation. As Dr.

Elena Vasilyeva, a computational trigonometry expert, explains: “The reference angle strips complexity to its essence. Working with π/4 avoids storytelling about quadrants and refocuses on values absolute—essential for algorithms, signal processing, and rotational dynamics.”

Applications span multiple disciplines. In signal processing, waveforms often repeat every 360° (2π radians); expressing shifts and amplitudes relative to 7π/4 simplifies Fourier analysis.

In physics, periodic motion such as pendulum swings or alternating currents rely on reference angles to model periodic behavior efficiently. Engineers use these benchmarks in control systems, where phase angles dictate torque and motor response. The 7π/4 angle itself appears in scenarios involving diurnal cycles or directional signal transmission, where 315° corresponds to northwest or southwest positioning—a critical reference for vector decomposition.

Calculating and applying the 7π/4 reference angle reveals more than a mathematical curiosity—it exemplifies how abstract values become actionable tools.

The route from radians to reference angle, from Quadrant IV placement to a clean π/4 baseline, showcases trigonometry’s elegance: precision through simplification. This reference angle is not merely numeric but conceptual—bridging geometry and computation. Whether teaching or applying, recognizing 7π/4’s reference angle empowers deeper insight into the periodic nature of real-world phenomena.

What once seems elusive—the 7π/4 reference angle—is now clear: 45 degrees, or π/4 radians, the anchoring benchmark that transforms angular complexity into mathematical fluency.

It stands not as a separation from standard angles, but as their refined extension—proof that even exotic angles yield harmony within the structured logic of trigonometry.