What Is an Equilateral Angle? Unlocking Symmetry in Geometry

When precision meets balance, the equilateral angle emerges as a foundational element in geometry—where symmetry, equality, and mathematical elegance converge. Defined not just by measurement but by intrinsic harmony, an equilateral angle is a cornerstone of spatial reasoning, deeply embedded in both theoretical frameworks and real-world applications. Its significance extends beyond textbooks, influencing architecture, engineering, and design through its embodiment of perfect proportionality.

The Core Definition: Equilateral and Its Angular Precision

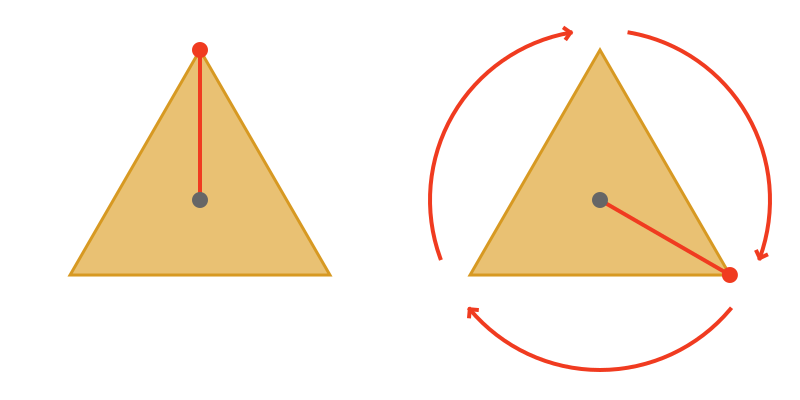
An equilateral angle is formally described as an angle whose two adjacent sides are of exact equal length—a defining feature in Euclidean geometry. While often associated with triangular structures, the concept applies specifically to angular relationships where both segments forming the angle measure the same length, although not all equilateral angles are confined to triangles. Mathematically, this equality in sides translates into congruent radii when visualized from the vertex, creating mirrored balance.

«The equilateral angle is nature’s signature of symmetry, a seamless fusion of form and function.» — Dr. Elena Marquez, professional geometrist and educator. This equality ensures the angle’s apex exhibits peak symmetry: rotating the vertex by 120 degrees or repositioning the arms produces identical orientations.

Unlike general angles measured in degrees, the equilateral angle is inherently tied to the regularity of its constructing triangle—typically equilateral, where all three sides and angles measure 60 degrees.

Mathematical Foundations and Measuring Equilateral Angles

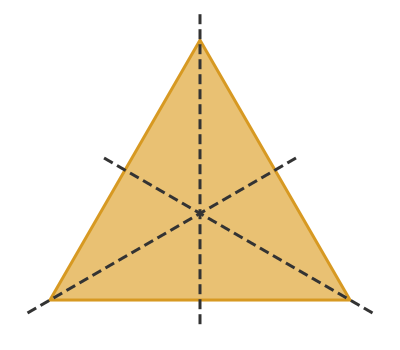
In standard mathematical terms, each angle in a perfect equilateral triangle measures 60 degrees, so by definition, all three internal angles are both equal and equilateral. This creates a system of predictable symmetry: - Each angle = 60° - All sides equal ⇒ vertex congruence - Rotational symmetry of order 3 (120°, 240°, 360° rotations maintain identical appearance) The equilateral angle behaves consistently across geometric constructions.

Whether used in isosceles or equilateral triangles, its 60-degree measure ensures stability in tessellations and tiling patterns, where repeated application produces seamless, uniform surfaces. This consistency makes it indispensable in fields requiring precise angular alignment, from CAD modeling to architectural blueprints.

Real-World Applications: From Architecture to Physics

Equilateral angles permeate practical domains, where their symmetry delivers both aesthetic appeal and functional efficiency.

In architecture, structures featuring equilateral angled elements—such as roof trusses or decorative facades—exhibit balanced weight distribution and visual harmony. The ancient Greeks, masters of proportion, employed equilateral configurations in temples to create enduring stability and elegance.

1. Civil Engineering: Trusses designed with 60-degree connections distribute load forces evenly across supporting members, reducing stress concentrations and enhancing durability.
2. Robotics and Automation: Jointed links often align at equilateral angles to enable smooth rotational motion and unidirectional movement paths.
3. Physics and Light Interference: In diffraction patterns and wave optics, equilateral angular relationships generate predictable, symmetric energy distributions.

These applications underscore the equilateral angle’s role as a silent architect of order—ensuring balance in complex systems where precision is paramount.

Equilateral Angle vs. Equiangular Angle: Clarifying the Distinction

While frequently confused, equilateral and equiangular angles serve distinct geometric functions. An equilateral angle demands equal side lengths, whereas an equiangular angle features equal measures, regardless of side proportion.

For instance, consider a quadrilateral where all interior angles are 90 degrees—each angle is equiangular but sides vary, making it rectilinear yet not equilateral. The equilateral angle’s strict adherence to side equality provides a unique geometric signature, whereas equiangular angles focus solely on degree measure symmetry. This distinction is critical in design: rotating an equilateral angle invariantly restores visual coherence, while equiangular configurations depend on external alignment for balance.

The Role in Regular Polygons and Advanced Patterns

Beyond triangles, equilateral angles define the structure of regular polygons—shapes where all sides and angles are congruent. A regular hexagon, for example, comprises six equilateral angles, each measuring 120 degrees at the center but formed by two equal-length radii. This angular precision enables the tessellation of flat planes without gaps, a principle exploited in tile design, molecular crystallography, and satellite antenna arrays.

In carbon hexagonal structures, such as fullerenes, molecular bonds arrange in equilateral triangular subunits, linking geometric theory to chemical stability. The angular symmetry ensures optimal electron distribution and structural resilience, highlighting mathematics’ quiet dominance in natural design.

Visualizing Equilateral Angles: Symmetry in Practice

Diagrammatically, an equilateral angle is best represented as a vertex flanked by two rays extending equal distances from the center.

Example constructions include: - Drawing an equilateral triangle, then measuring each internal angle to confirm 60°. - Using a 60° angle finder tool to verify