<strong>Unlocking the Power of Antiderivatives: How Trigonometric Integrals Power Engineering, Physics, and Data Science</strong>
Unlocking the Power of Antiderivatives: How Trigonometric Integrals Power Engineering, Physics, and Data Science
Antiderivatives of trigonometric functions form a cornerstone of calculus with profound implications across science, engineering, and mathematics. These integrals underpin everything from calculating areas under curved data plots to modeling wave behavior in physics and refining optimization algorithms in machine learning. Unlike basic derivatives, antiderivatives—also known as indefinite integrals—capture cumulative effects, transforming instantaneous rates into total accumulation.
From the sine and cosine functions to tangent and secant, each trigonometric antiderivative holds unique patterns, techniques, and real-world significance.
The Core: Prime Facts About Antiderivatives of Sine and Cosine
At the heart of trigonometric integration lie two fundamental antiderivatives: ∫sin x dx = –cos x + C and ∫cos x dx = sin x + C. These simple results arise from reversing differentiation—observing that the derivative of –cos x is sin x, and of sin x is –cos x—establishing a rhythmic, self-consistent structure. “This symmetry is elegant,” notes Dr.
Elena Marquez, calculus educator at MIT. “Just as sine and cosine interlock in the unit circle, their integrals mirror that connection—one shifted, one flipped.”
What makes these integrals uniquely suited for application is their periodic nature—repeating every 2π units—which makes them ideal for modeling cyclic phenomena. “In physics, integrating velocity (ms⁻¹) yields displacement (m), and trig antiderivatives formalize this cumulative motion,” explains mechanical engineer James Tran.
“Without them, describing oscillatory systems would be computationally intractable.”
Step-by-Step: Solving ∫sin x dx and ∫cos x dx
- Start with ∫sin x dx: recall that differentiation of –cos x produces sin x, by inverse relationship, so –cos x is a natural antiderivative.
- Similarly, ∫cos x dx leverages that cos x is itself the derivative of sin x; hence, ∫cos x dx = sin x + C.
- Always include the constant of integration (C), reflecting the infinite family of functions differing only by vertical shifts.
- These basic forms extend to composite trigonometric expressions—driving more complex integrals through substitution, integration by parts, or trigonometric identities.
Advanced Techniques: Integrating Products and Powers of Trigonometric Functions
While ∫sin x and ∫cos x are straightforward, most real-world problems demand deeper methods. Consider ∫sin²x dx—appearing frequently in signal processing. Naively failing to integrate directly, one uses the identity sin²x = (1 – cos 2x)/2, reducing the power via a double-angle transformation: ∫sin²x dx = ∫(1 – cos 2x)/2 dx = (1/2)x – (1/4)sin 2x + C.
“This identity-based substitution isolates the oscillatory component,” details prof. Rajesh Iyer. “It reveals structure hidden in the original expression.”
Similarly, integrals like ∫tan x dx or ∫sec x dx do not return to elementary elementary functions.
Instead, tan x = sin x/cos x prompts substitution: let u = cos x, so du = –sin x dx. The integral becomes –∫(1/u) du = –ln|cos x| + C. For ∫sec x dx, rationalizing via sec x = sec x·(sec x + tan x)/(sec x + tan x) leads momentarily to –ln|sec x + tan x| + C—a result pivotal in electrical engineering for analyzing alternating current circuits.
Real-World Applications: Where Antiderivatives Drive Innovation
The utility of trigonometric antiderivatives extends far beyond academic exercises.
In signal processing, Fourier transforms decompose waves into sine and cosine components, with integrals underpinning frequency analysis. This drives everything from audio compression in MP3s to MRI imaging in medicine. In orbital mechanics, integration of elliptic trigonometric integrals predicts planet and satellite trajectories with precision.
“Precise modeling of planetary motion depends on these integrals,” says space physicist Dr. Lena Torres. “They account for gravitational perturbations—tiny but critical over long periods.” Even machine learning relies subtly: optimization algorithms often involve periodic loss functions or rotating vector fields modeled through trig integrals.
Whether shaping advanced robotics or climate models, the foundational antiderivative of sine x powers computational core systems.
The Underlying Unity: Why Trigonometric Integrals Resist Simplification
What makes trigonometric antiderivatives enduring is their inherent complexity despite elegant form. “These functions resist over-simplification because their integrals encode periodic behavior, which inherently demands nonlinear, piecewise-defined solutions,” observes Dr. Marquez.
“Unlike exponential or polynomial functions, trigonometric integrals preserve oscillation, symmetry, and rotational invariance through every transformation.”
This mathematical resilience ensures antiderivatives remain vital: each appears not as a standalone skill but as a gateway. Mastery enables tackling the 제품 of trigonometric and algebraic expressions, extending applications into quantum mechanics, navigation systems, and financial time-series forecasting. The cycle repeats—each applied problem reinforces core principles, transforming raw formulas into intuitive understanding.
In essence, antiderivatives of trigonometric functions are more than mathematical curiosities.
They encapsulate the dance between repetition and accumulation, motion and memory. From classroom warm-ups to cutting-edge research, their antiderivatives stand as silent architects of modern technological progress—proving that even the most ancient calculus tools remain indispensable in the digital age.
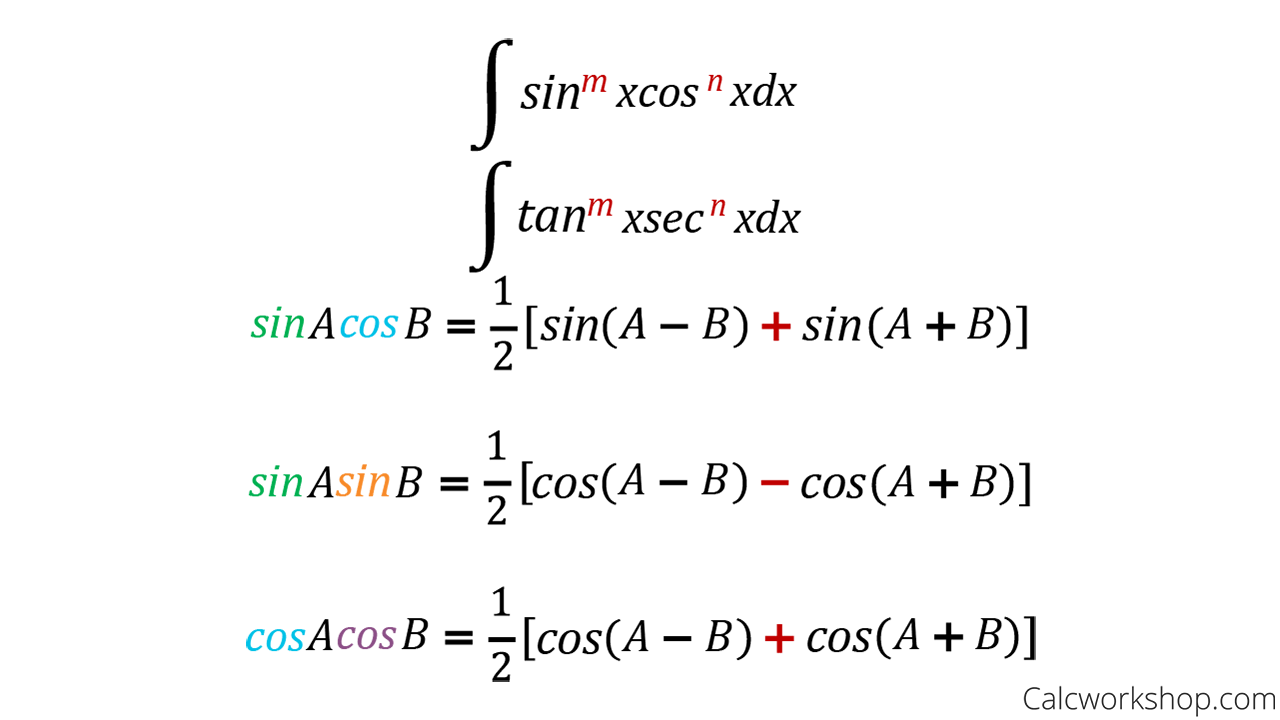


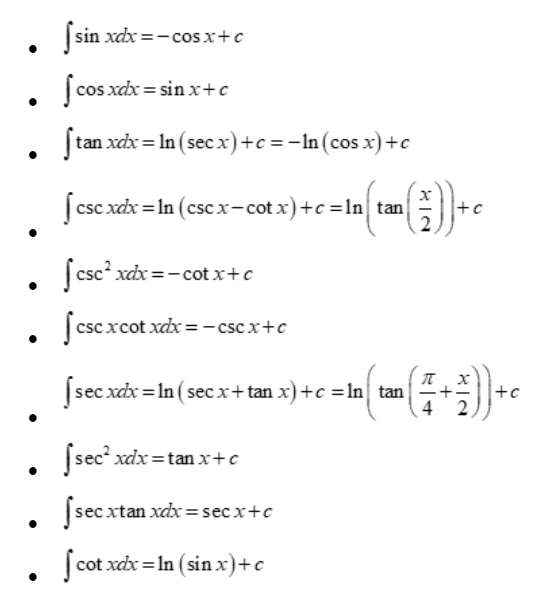
Related Post
Nicole Drinkwaters’ Onlyfans Journey: The Shocking Truth Behind the Platform and the Personal Cost

Man City vs. Liverpool: Who’s the Richest Club in the Premier League Battle?

