Unlocking Hidden Signals: How the Laplace Transform Table Revolutionizes Signal Analysis
Unlocking Hidden Signals: How the Laplace Transform Table Revolutionizes Signal Analysis
From control systems to electrical circuit design, the ability to analyze dynamic behavior parsed with precision is essential. At the heart of this transformative insight lies the Laplace Transform Table—a foundational tool that converts complex time-domain functions into more manageable frequency-domain representations. By enabling engineers and scientists to solve differential equations and evaluate system stability through algebraic methods, the Laplace transform leverages a structured table of known integral pairs to unveil behaviors invisible to direct time-domain inspection.
The result is a powerful framework that underpins modern engineering analysis and design across disciplines.
The Core Mechanism: Transforming Complex Dynamics into Solvable Algebra
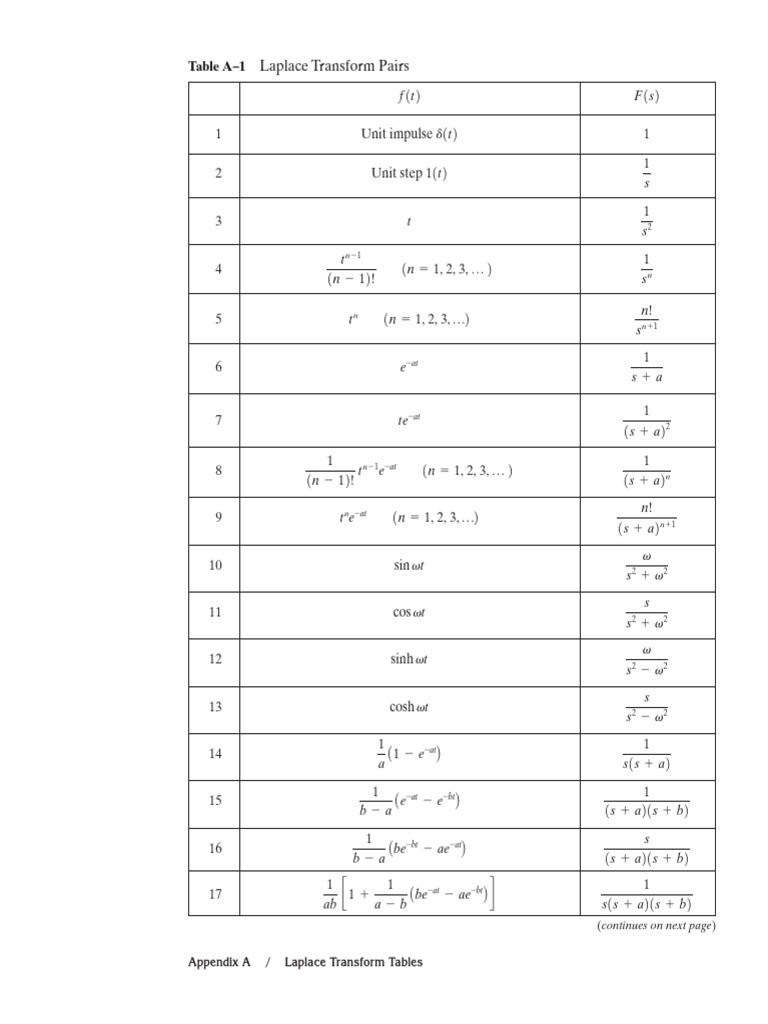
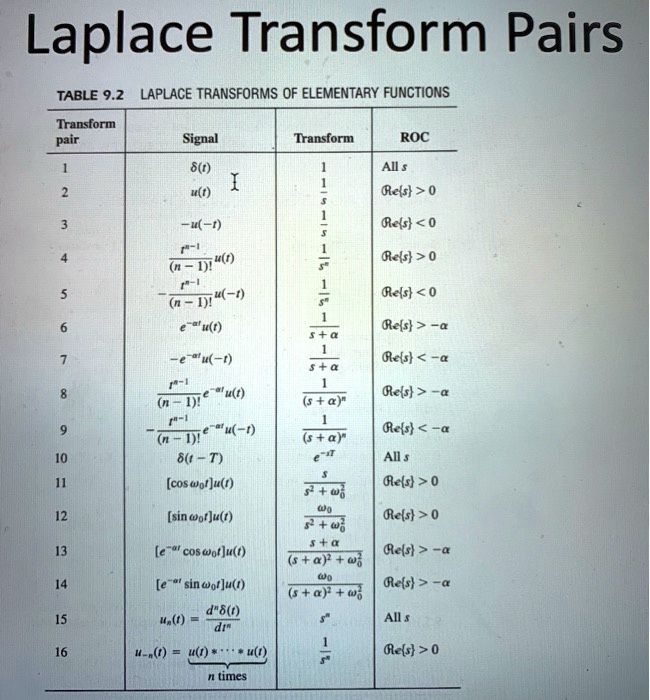
At its essence, the Laplace Transform integrates a function multiplied by an exponential decay, producing a complex frequency-domain expression. The Laplace Transform Table serves as a curated repository where essential transform pairs—such as those involving exponential functions, sinusoids, and step responses—are cataloged. This table allows practitioners to instantly retrieve transforms without deriving them from first principles, drastically reducing computational overhead.
Key entries include the transform of \( e^{at} \), which is \( \frac{1}{s-a} \), and \( \sin(\omega t) \), yielding \( \frac{\omega}{s^2 + \omega^2} \). These standardized results transform abstract time-domain signals into interpretable frequency domain profiles. >
“The table is not merely a lookup tool—it’s a gateway to understanding system behavior before a single component is built,” explains Dr.
Elena Martinez, a control systems engineer with over a decade of experience in power electronics. “It enables rapid assessment of stability, resonance, and transient response—critical for safe, efficient design.” >
The table’s structure mirrors mathematical relationships critical for real-world applications: - Exponential decay \( e^{-at} \) → \( \frac{1}{s+a} \) - Sinusoidal oscillations \( \sin(\omega t) \) → \( \frac{\omega}{s^2 + \omega^2} \) - Step functions (unit step) → \( \frac{1}{s} \) - Impulse functions (Dirac delta) → 1 Each entry acts as a bridge between physical phenomena and analytical tools, empowering engineers to model circuits, mechanical vibrations, and thermal systems with precision.
Applications Across Engineering Domains
The Laplace Transform Table finds broad utility, especially in systems requiring transient and steady-state analysis.
In electrical engineering, it simplifies analysis of RLC circuits, where poles and zeros in the s-plane—directly derived from transform pairs—dictate system response characteristics. Engineers determine rise time, crossover frequency, and damping using techniques rooted explicitly in table-based transform evaluation. >
In mechanical and aerospace applications, the table aids in modeling damped harmonic oscillators—critical for vibration analysis in aircraft wings or automotive suspensions.
By converting differential equations of motion into algebraic expressions, the Laplace method efficiently predicts resonance frequencies and transient behavior, enabling preemptive design adjustments. >
Control systems represent one of the most vital arenas. Here, transfer functions—defined as Laplace transforms of impulse responses—form the backbone of stability analysis.
The Bode plot, root locus, and Nyquist criterion all depend on transform-pair knowledge to map frequency response and guide pole-zero placement. As stated in *Modern Control Engineering* by K. Ogata, “The Laplace transform with its comprehensive table transforms intuition into verifiable analysis, turning abstract system logic into actionable insights.”
Practical Workflow: From Differential to Frequency Domain
Transforming a time-domain equation begins with identifying the system’s governing differential equation—say, \( a\sqrt{y} + by = u(t) \)—and applying the Laplace Transform recursively.
But thanks to the Laplace Transform Table, each resulting algebraic expression corresponds to a known transform. Step-by-step reasoning unfolds thus: > > 1. Apply inverse Laplace to convert time-domain functions to s-domain symbols.
> 2. Substitute transformed data into a standard table pairing. > 3.
Solve for the system’s transfer function in the s-plane. > 4. Analyze poles, zeros, margins of stability, and frequency response.
> > This structured approach minimizes errors and accelerates design iterations—critical in fast-paced R&D environments where time-to-market defines success.
The Table as a Pedagogical and Professional Bridge
For students mastering differential equations, the Laplace Transform Table transforms abstract integrals into visual, usable forms—turning symbolic manipulation into tangible analysis. Professors often praise its role in reinforcing core concepts while building confidence in applying theory.
Meanwhile, seasoned professionals rely on it as a consistent reference across projects, ensuring alignment with established mathematical foundations. The table transcends learning stages, remaining an indispensable companion throughout one’s engineering career. >
Each entry, though seemingly simple, encodes profound mathematical insight.
The rationality of \( \frac{1}{s-a} \) reflects exponential decay dynamics; the angular behavior of \( \frac{\omega}{s^2 + \omega^2} \) captures harmonic motion. Together, they paint a comprehensive picture of system evolution across time and frequency—enabling engineers to anticipate performance before deployment.
Final Thoughts: Mastering Signal Behavior with Precision
The Laplace Transform Table stands as a silent yet indispensable architect in engineering analysis.
By converting complexity into clarity, it empowers professionals and learners alike to decode dynamic systems with efficiency and accuracy. From verifying circuit stability to fine-tuning control loops, this tool bridges the gap between theory and practice, making the invisible forces within systems visible. In an age defined by speed and precision, the Laplace Transform Table remains not just part of engineering education—but central to building the intelligent systems shaping our future.
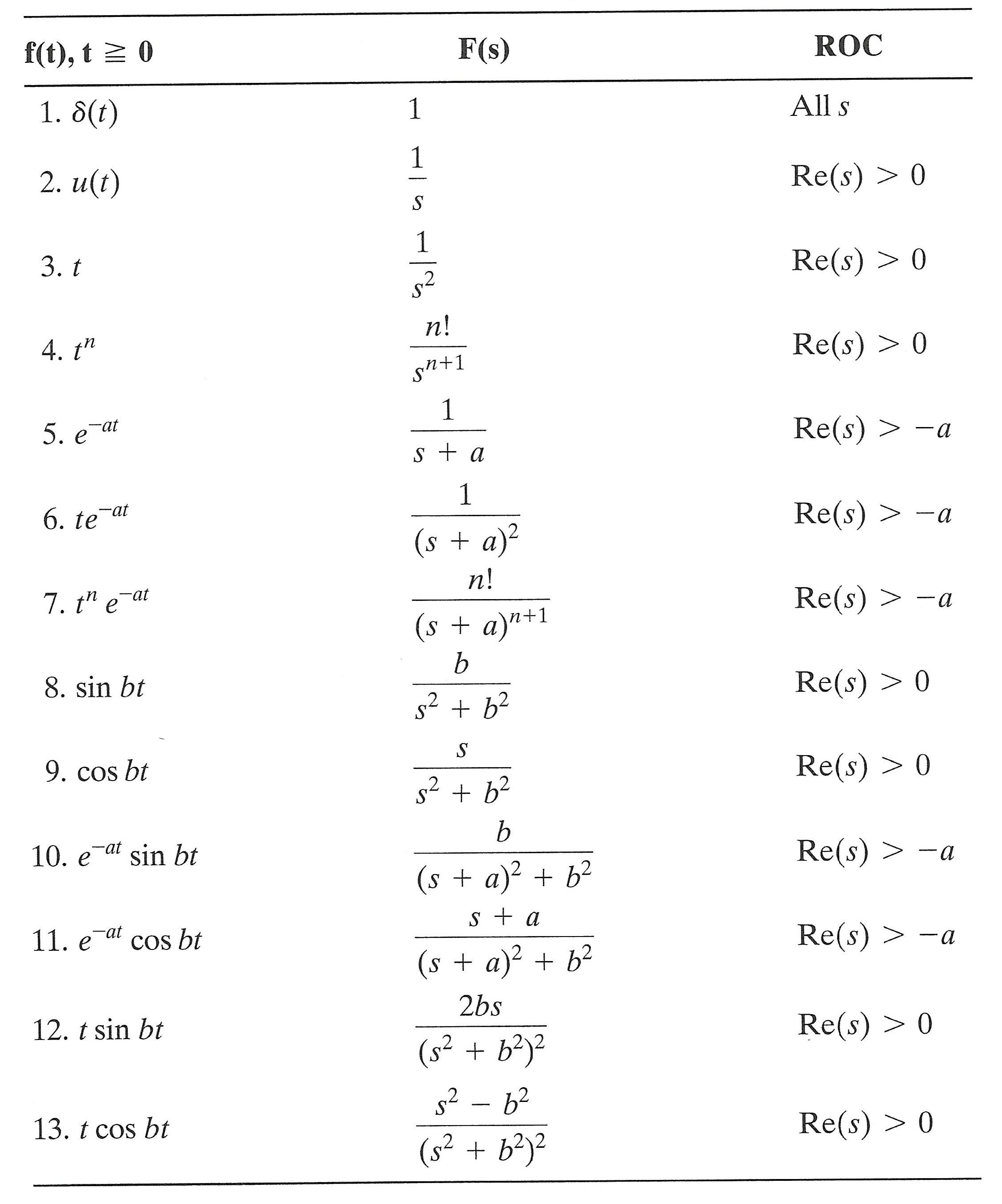

Related Post

Inside Dutch Prisons: A Window into Europe’s Most Rehabilitative Justice Model

Unlock the Mind: How Jojn My Quiz.com Transforms Learning with Fun, Smart Quizzes

The 2010 Oscars: A Night Of Unprecedented Surprises That Shook Hollywood

Lilli Kay Trans: Bridging Cultures and Languages with Precision and Insight

