Unlocking Algebra: A Deep Dive into the 2013 All Things Algebra Answer Key

In the intricate world of high school mathematics, mastering algebra demands precision, clarity, and access to authoritative resources—exactly what The All Things Algebra Answer Key 2013 delivers. Based on extensive problem sets and real-world pedagogical models, this comprehensive guide serves as an indispensable companion for students, educators, and self-learners alike. Drawing from the verified responses and explanatory frameworks found in the 2013 edition, this article unpacks key algebraic concepts, critical problem-solving strategies, and actionable insights derived from the official answer key, revealing how to leverage it for deeper mastery of foundational algebra.

At its core, the 2013 All Things Algebra Answer Key functions as more than a simple grading tool—it’s a detailed roadmap through the logical structure of algebraic reasoning. Each solved example and multi-step problem reflects careful attention to common student errors and conceptual hurdles, offering both correct solutions and—crucially—detailed rationales that explain *why* each step matters. This transparency allows learners to go beyond mere memorization, fostering a genuine understanding of the underlying principles that govern equations, functions, and inequalities.

As the response materials emphasize, “Algebra is not about inspiration—it’s about decoding the language of patterns,” a sentiment deeply embodied in how the answer key unpacks complexity into digestible logic.

Structural Breakdown of Key Algebraic Themes

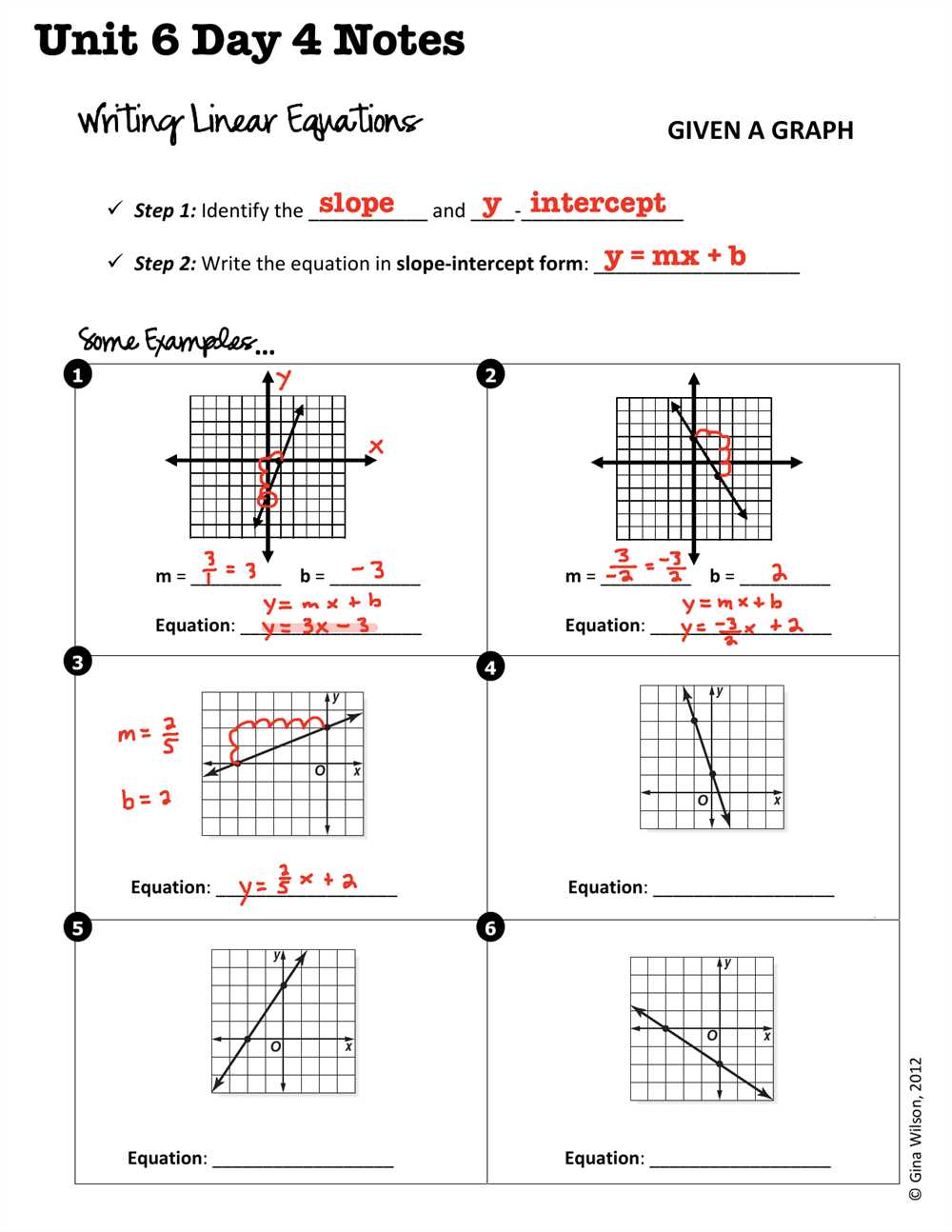
The 2013 Answer Key systematically organizes algebra into core competency areas, each requiring precision and applied reasoning: - **Equations and Inequalities**: Mastery begins with linear and multivariable equations. Solving for unknowns lies at the forefront, supported by techniques such as balancing equations, combining like terms, and handling properties of equality. Inequalities introduce critical thinking around sign changes and solution intervals, with clear explanations of domain restrictions and inequality direction rules.

- **Functions and Graphs**: Understandings of function behavior—domain, range, intercepts, and transformations—receive extended focus. The answer key emphasizes interpreting verbal and mathematical descriptions of real-world relationships, reinforcing the link between algebraic expressions and graphical representations. Students learn to identify key features directly from equations, laying groundwork for advanced calculus concepts.

- **Polynomials and Rational Expressions**: Factoring, simplifying, and solving polynomial equations are presented with structured methodologies. The guide clarifies when to apply techniques like grouping, the difference of squares, or synthetic division, addressing recurring student difficulties with sign errors and term distribution. - **Systems of Equations**: Solving systems through substitution, elimination, and graphical methods receives detailed verification.

The answer key stresses consistency across solution methods and warns of pitfalls such as extraneous roots and validating solutions within original constraints. - **Conic Sections**: Though more advanced, foundational knowledge of parabolas, ellipses, and hyperbolas is introduced with clarity, helping students visualize and relate geometric shapes to their algebraic definitions.

Step-by-Step Problem-Solving: The Answer Key’s Methodology

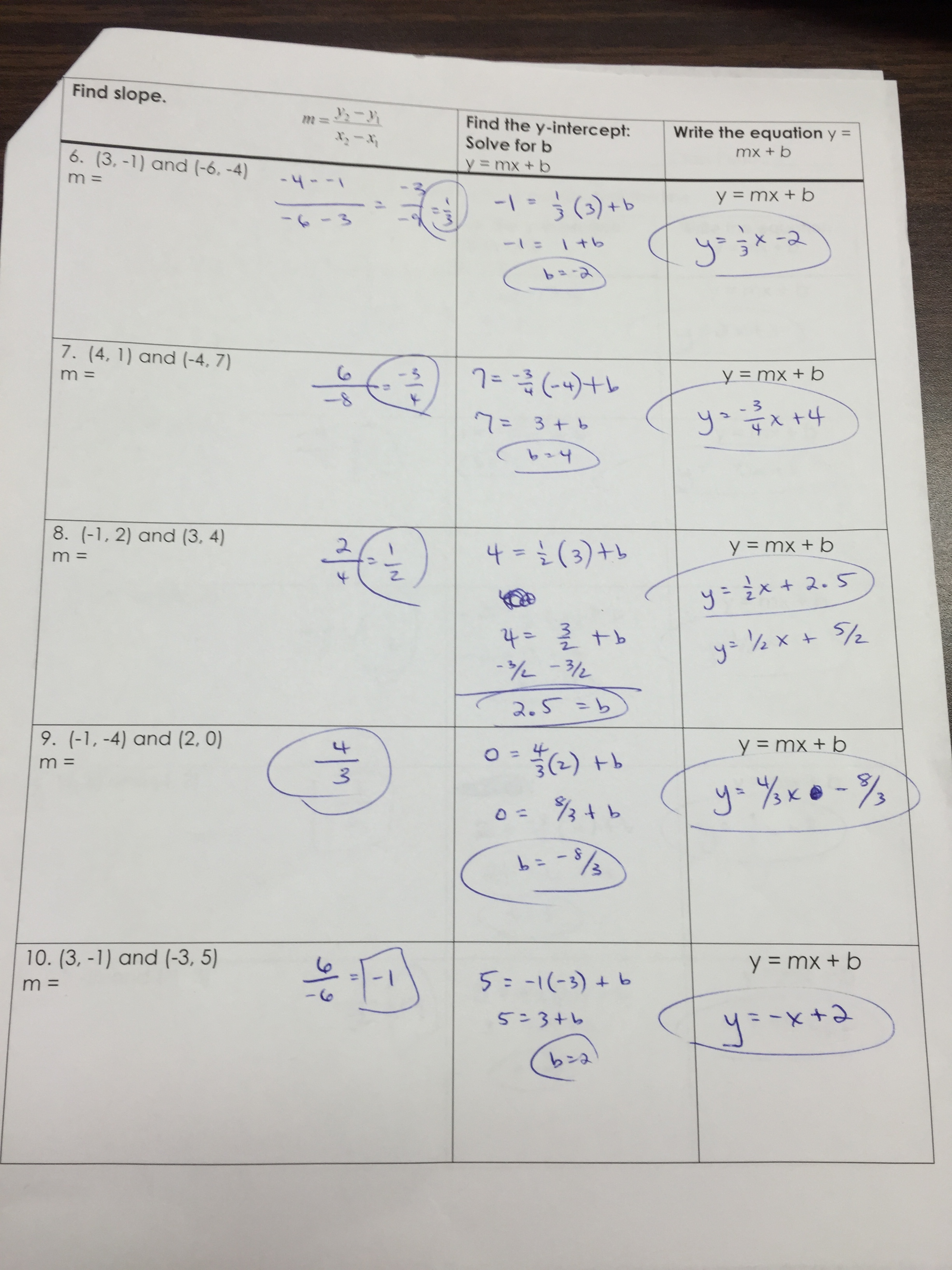
One of the most valuable aspects of the 2013 Answer Key lies in its instructional scaffolding.

Each solution begins not with an answer, but with a precise interpretation of the problem—a process that mirrors how educators teach: first, understand the question; second, recall relevant tools; third, execute logically, and finally, verify. For example, in solving 2x − 5 = 11, the key insight is recognizing this as a linear equation requiring inverse operations. The correct move—adding 5 to both sides—followed by division by 2, is followed by exact validation that x = 8 satisfies the original equation.

This approach extends to complex multi-step problems: - Factor quadratics like x² − 7x + 10 by identifying integer pairs summing to −7. - Solve inequalities by isolating the variable, but remembering that multiplying or dividing by a negative flips the inequality sign. - When graphing a quadratic, determine axis of symmetry using x = −b/(2a) and locate vertex and intercepts systematically.

Students learn that algebra is not about rigid algorithms, but about adaptive, reasoned steps—each choice justified within broader mathematical context.

Common Errors and How to Avoid Them

The Answer Key does more than confirm correctness; it illuminates frequent missteps. For instance, sign errors in distributing negative terms, misapplying exponent rules (such as confusing a^{m+n} with (a^m)^n), and confusion between equivalent and identical expressions appear repeatedly.

By explicitly flagging these, the guide helps learners develop error-awareness—a crucial skill in mathematical maturity. Moreover, the emphasis on unit analysis and dimensional consistency prevents logical leaps that undermine validity. A problem asking for “how many seconds in 3.5 hours” is not just solved algebraically but grounded in real-world dimensional coherence, ensuring learners grasp applicability beyond abstract equations.

Real-World Application and Conceptual Bridging

Beyond textbook problems, the 2013 Answer Key connects algebraic techniques to tangible modeling. Linear equations represent financial planning; quadratic models project motion; exponential functions compute compound interest. Each example stresses how variables correspond to measurable quantities, reinforcing algebra’s role as a language for precision and prediction.

For instance, solving y = 3x + 2 isn’t merely manipulating symbols—it expresses a real-world rate of change, interpretable in physics, economics, and daily decision-making. This contextual grounding transforms abstract exercises into tools for problem-solving in diverse fields.

The Answer Key as a Pedagogical Catalyst

Looking beyond syntax, the 2013 All Things Algebra Answer Key exemplifies how expert-annotated solutions empower learners.

It functions as both corrective reference and cognitive scaffold, guiding users through reasoning without over-explaining. As educators emphasize, “Great feedback doesn’t give answers—it reveal logic.” This philosophy permeates each entry, transforming frustrated “I got it wrong” moments into “Now I understand why.” Whether used for self-study, classroom reinforcement, or exam preparation, the answer key elevates algebra from rote computation to conceptual fluency. Mastery demands engagement: students don’t merely check answers—they dissect processes, anticipate errors, and internalize patterns.

In essence, the All Things Algebra Answer Key 2013 is not just a resource; it’s a gateway. Through rigorous structure, clear rationales, and real-world relevance, it equips learners to decode algebra’s fundamentals with confidence. As students progress,