Transforming Space: Mastering Cartesian to Spherical Coordinates with Precision

Converting between Cartesian and spherical coordinate systems is a foundational skill in applied mathematics, physics, engineering, and computer graphics—enabling accurate spatial representation across disciplines. This transformation unlocks efficient solutions for problems involving symmetry, radial distance, angular orientation, and complex vector analysis. As data modeling and 3D rendering grow more sophisticated, understanding how Cartesian coordinates (x, y, z) map to spherical counterparts (ρ, θ, φ) becomes indispensable for professionals and researchers alike.

The Essentials of Coordinate Transformation

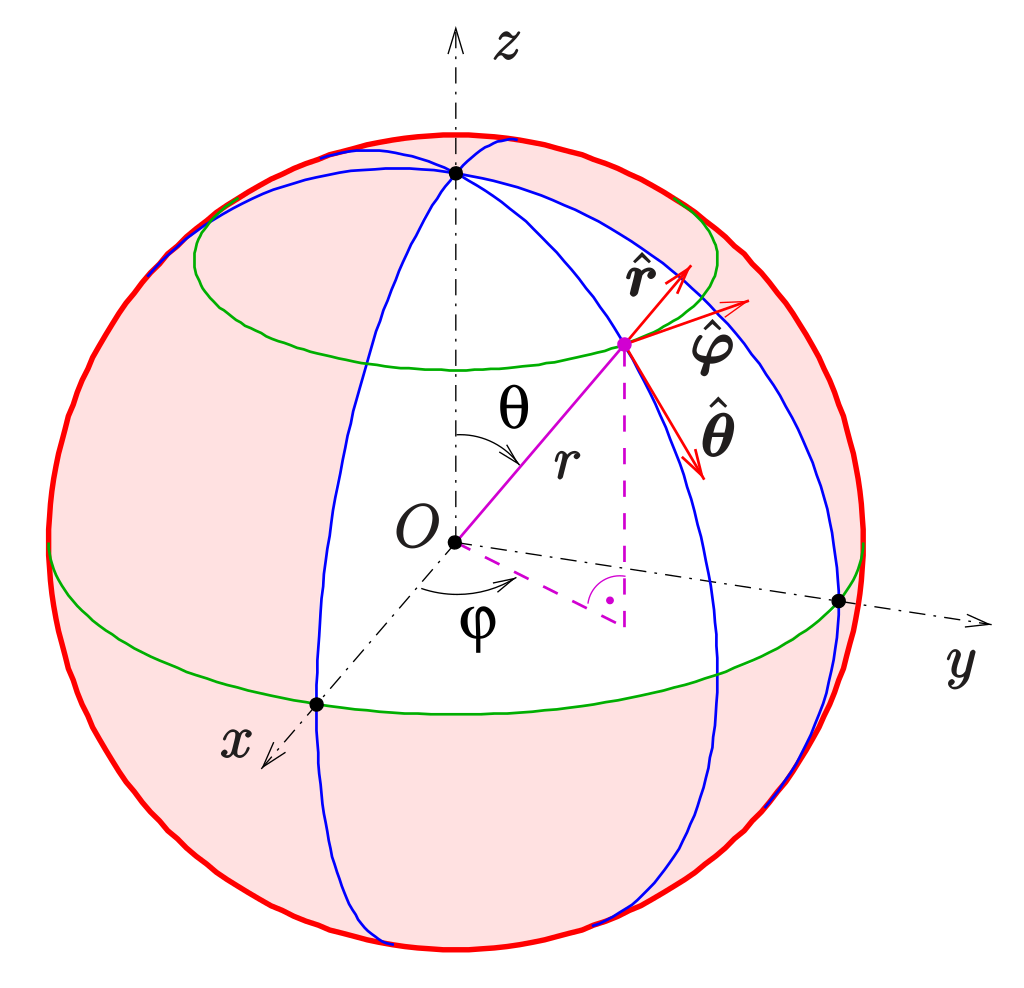
Spherical coordinates provide a powerful alternative to Cartesian systems by describing points in 3D space using radial distance, polar angle, and azimuthal angle.

This system excels in spherical symmetry environments—such as radiation patterns in electromagnetics, celestial mechanics, or medical imaging—where Cartesian expressions grow unwieldy. The transformation equations, derived from Pythagorean and trigonometric principles, serve as an essential bridge between Cartesian simplicity and spherical context. The mathematical transformation from Cartesian (x, y, z) to spherical (ρ, θ, φ) is defined by: ρ = √(x² + y² + z²) θ = arccos(z / ρ) — inclination from positive z-axis φ = arctan(y / x) — azimuthal angle in xy-plane from positive x-axis (with quadrant handling) These relationships convert Cartesian space into a hierarchical structure where radial movement dictates proximity, the polar angle defines elevation, and azimuth specifies horizontal orientation.

“Any transformation into spherical coordinates simplifies problems intrinsically linked to symmetry around a point,” states Dr. Elena Marquez, a computational physicist at MIT, “especially when volume integration or field propagation is involved.”

Core Transformation Formulas Explained

The transformation hinges on three critical components, each revealing a distinct geometric relationship: – **Radial Distance (ρ):** This scalar value quantifies the shortest straight-line distance from the origin (0, 0, 0) to the point (x, y, z). Derived from the 3D Pythagorean theorem, ρ = √(x² + y² + z²) forms the first layer of spatial mapping—akin to measuring a full umbrella’s spread from center to edge.

– **Polar Angle (θ):** Often called the colatitude, θ measures the angle upward or downward from the North (positive z) axis. Using θ = arccos(z / ρ), this angle defines vertical alignment. When z = 0, φ becomes undefined—a hallmark of equatorial planes where azimuth overwhelms elevation distinction.

– **Azimuthal Angle (φ):** This lateral angle measures rotation about the z-axis, ranging from 0° to 360° (or –180° to 180°). Defined by φ = arctan(y / x), careful handling of the quadrant—via built-in driver functions in numerical libraries—is essential to avoid misalignment, particularly near the axes. Together, these equations transform the Cartesian triad into spherical representations that align with physical intuition in radially symmetric domains.

Applications Across Science and Technology

The Cartesian-to-spherical conversion finds utility in diverse, high-impact domains: – **Physics & Electromagnetics:** Radiation intensity from antennas or point sources follows spherical spreading. Engineers use ρ to model field decay (∝ 1/ρ²), while θ and φ define directional patterns. As physicist James Holloway notes, “in antenna design, spherical coordinates allow engineers to visualize beam shapes in full 3D space.” – **Astronomy:** Celestial objects are mapped using Right Ascension and Declination—spherical analogs—to track positions across the sky.

This convention supports accurate orbit calculation and telescope targeting. – **Computer Graphics & Visualization:** 3D environments rely on spherical coordinates for particle systems, camera rotations, and level-of-detail rendering. Gl Mapping libraries often convert object positions from world space (Cartesian) to camera-view space (spherical) via efficient coordinate transformation.

– **Medical Imaging:** CT and MRI scans reconstruct 3D body data using spherical harmonics and coordinate re-mapping. Accurate conversion supports tumor localization and surgical planning from volumetric scans. “Without reliable Cartesian-to-spherical conversion, rendering realistic spherical scenes or modeling radial phenomena would require exponentially more computational overhead,” explains Dr.

Lin Zhang, a research scientist at NASA’s Jet Propulsion Laboratory.

Overcoming Challenges in Conversion

Despite their utility, Cartesian-to-spherical transformations introduce subtle pitfalls demanding attention. Foremost among these is singularity in φ when x = 0 and y = 0: both z and x determine φ’s quadrant, requiring conditional logic to assign correct sign.

Additionally, numerical precision degrades when ρ ≈ 0 due to division by near-zero values in θ = arccos(z / ρ), necessitating careful error handling in software. Handling undefined cases—such as division by zero or angle ambiguity—requires robust validation. Libraries like NumPy and MATLAB implement built