The Derivative of Inverse Trig: Unlocking Precision in Calculus and Beyond
The Derivative of Inverse Trig: Unlocking Precision in Calculus and Beyond
Inverse trigonometric functions are indispensable tools in calculus, engineering, physics, and data science—but their derivatives remain among the most debated and underappreciated constructs in mathematical analysis. Deeply woven into the fabric of modern problem-solving, the derivative of inverse trig functions enables precise modeling of angular relationships, growth curves, and dynamic systems where angles evolve over time. From determining tangent lines to inverse sine for angular velocity, mastering this derivative unlocks a deeper fluency in calculus applications—bridging pure theory with real-world utility.
The Core Formula: Defining the Derivative of Inverse Sine and Cosine
At the heart of inverse trigonometric calculus lies a set of well-defined derivatives that follow algebraic patterns rooted in differentiation rules.
The derivative of the inverse sine function, denoted as y = sin⁻¹(x), is grounded in implicit differentiation and the composition rule:
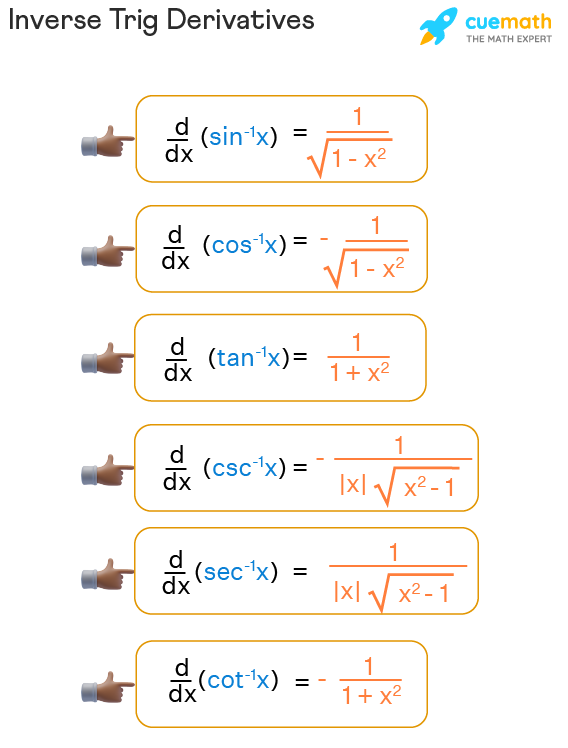
dy/dx = 1 / √(1 − x²)
This expression emerges from differentiating both sides of sin(y) = x with respect to x, yielding x·dy/dx = 1/√(1 − x²), which rearranges to the famous formula. Similarly, for the inverse cosine function, y = cos⁻¹(x), the derivative is:
dy/dx = −1 / √(1 − x²)
The contrasting sign in cos⁻¹ reflects a decreasing behavior of cosine in its principal domain, ensuring derivative consistency with function behavior. These derivatives are not merely notational exercises—they encode essential information about rate of change under angular arcs, critical in fields from robotics to signal processing.
Derivatives of Other Inverse Trig Functions: A Comparative View
While sine and cosine derivatives dominate introductory calculus, inverse tangent (arctangent) derivatives reveal key structural insights.
For y = tan⁻¹(x), differentiating implicitly from tan(y) = x leads to:
dy/dx = 1 / (1 + x²)
This rational form simplifies integration and optimization problems involving slopes—arctangent’s derivative underpins many neural network activation functions and feedback control systems. Similarly, inverse secant and inverse cotangent derivatives follow analogous implicit patterns, though less frequently taught, their structures reinforce the symmetry and continuity across inverse trig functions.
Geometric Interpretation: Derivatives as Steepness of Inverse Curves
Geometrically, these derivatives represent instantaneous slope rates of inverse trigonometric curves. For example, d/dx[sin⁻¹(x)] = 1/√(1 − x²) captures how steeply the angle of a unit circle’s arc changes as x increases.
As x approaches ±1, the denominator shrinks toward zero, reflecting unbounded slope growth—a key consideration in singularity detection. In the unit circle model, where x = sin(y), a small x shift near endpoints tightens y’s rate of change, mathematically formalized by the inverse derivative.
Applications Across Scientific and Engineering Domains
The derivative of inverse trig functions drives innovation in diverse fields:
- Physics:** In pendulum motion and rotational dynamics, inverse sine derivatives model angular displacement under restoring forces; arctangent derivatives describe velocity-phase relationships in AC circuits with phase shifts.
- Engineering:** Control systems use arctangent derivatives to compute angular velocity from position feedback, enabling smooth trajectory planning in robotics and drones.
- Computer Graphics and Computational Geometry:** When calculating curvature or arc-length approximations, inverse trig derivatives enable precise slope adjustments for curved elements in rendering engines and CAD software.
- Machine Learning:** Activation functions such as tanh implicitly rely on tan⁻¹ derivative principles for gradient-based optimization in neural networks, particularly in backpropagation through angular mappings.
Common Pitfalls and Best Practices
Despite their elegance, these derivatives are prone to frequent errors. A common mistake is forgetting the square root’s restricted domain: √(1 − x²) exists only for x ∈ [−1, 1], as inverse sine and cosine domains are |x| ≤ 1.
Misapplying the chain rule or mishandling negative signs in arctangent derivatives compounds inaccuracies, especially when composing inverse trig with polynomials or exponentials. To avoid errors, practitioners must rigorously enforce domain constraints and verify sign behavior across intervals, particularly when dealing with composite functions.
The Role of Inverse Trig Derivatives in Advanced Calculus
Beyond singular calculus problems, inverse trig derivatives underpin higher mathematical frameworks. In manifold theory, they define natural gradients on curved spaces; in differential equations, they model feedback loops with angular constraints.
Their appearance in Taylor and Fourier expansions underscores their role in approximation theory, enabling elegant representations of periodic and bounded functions. Understanding these derivatives not only strengthens computational fluency but also cultivates deeper insight into the geometric intuition behind calculus.
Mastering the Derivative of Inverse Trig: A Gateway to Precision
The derivative of inverse trigonometric functions is far more than a formula—it is a cornerstone of analytical thinking in mathematics and its applied disciplines. Through rigorous derivation, careful domain awareness, and deliberate application, these derivatives empower precise modeling of dynamic systems, from physical oscillations to machine learning algorithms.
In a world governed by curves and angles, fluency in inverse trig derivatives transforms abstract equations into actionable insight, proving that true mathematical mastery lies not just in computation, but in controlled, intentional reasoning.

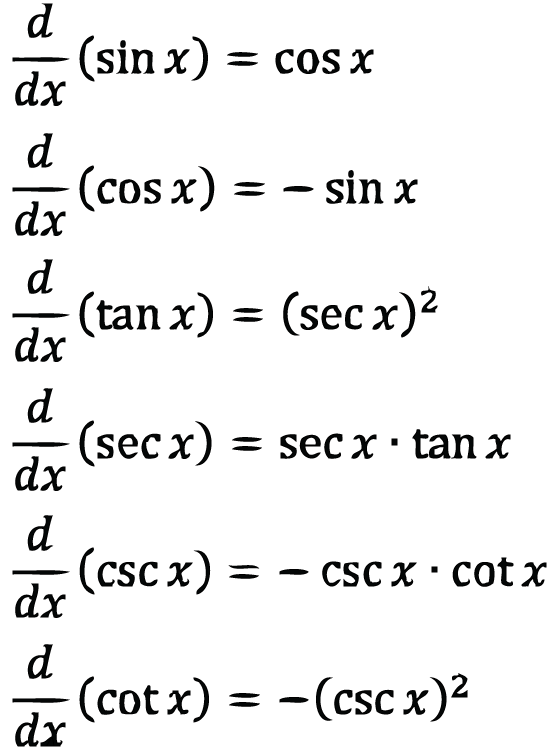
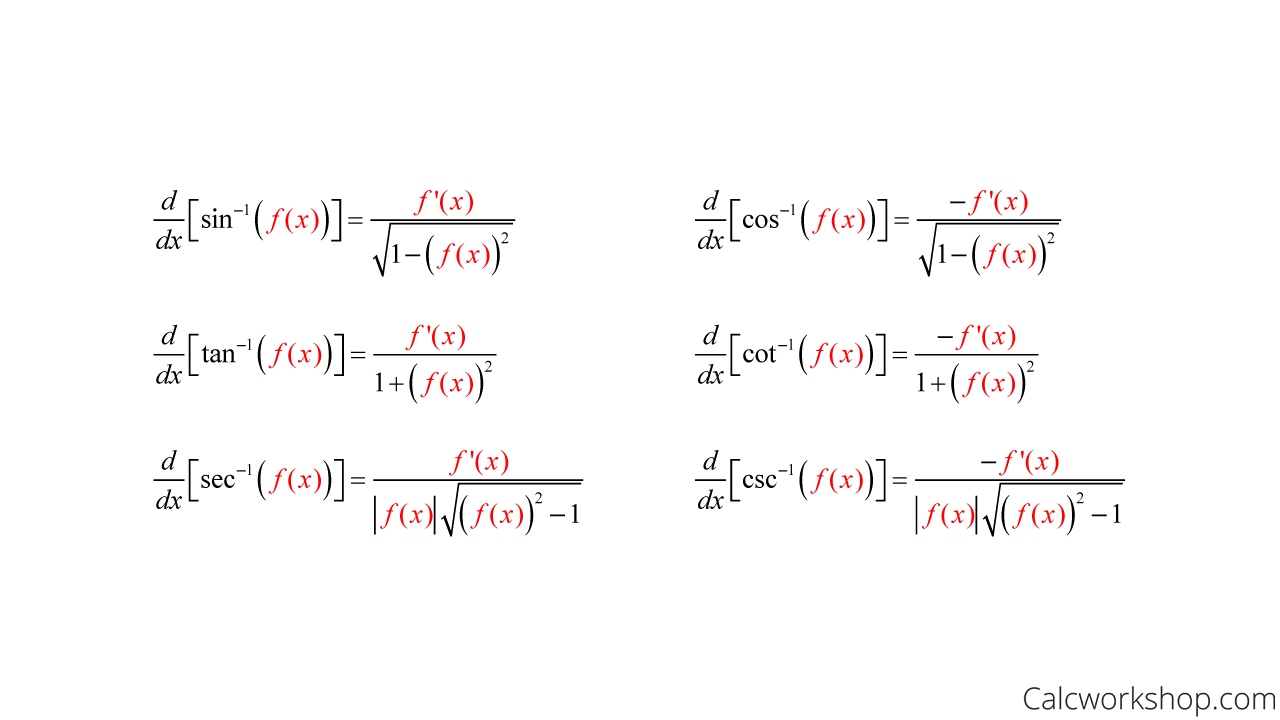
Related Post

Randy Moss’s Wife: The Quiet Strength Behind the Celtic Legend

Unveiling The Power Demons Of The Upper Moons and Hantengu: Legends of Shadow and Cosmic Might

Unlock Your Drive: How Santander Auto Loan Login Shapes Modern Car Financing

Calgary Timezone: Precision, Practice, and Precision in a Global City Across Time Zones

