Multiplication Property of Equality: The Mathematical Key to Balance and Consistency
Multiplication Property of Equality: The Mathematical Key to Balance and Consistency
When equations hold firm under transformation, the multiplication property of equality emerges as a foundational truth in algebra and beyond—guaranteeing that multiplying both sides of an equation by the same non-zero number preserves equality. This principle, simple in expression but profound in application, enables precise reasoning across mathematics, physics, and engineering. By exploring its mechanisms, implications, and real-world use, we uncover how this property underpins consistency in problem-solving.
The multiplication property of equality states: If \( a = b \), then \( a \cdot c = b \cdot c \) for any scalar \( c \) not equal to zero.
This rule is not merely algebraic mumbo-jumbo—it reflects a deep logical structure of equality itself. Unlike substituting values arbitrarily, multiplying both sides equally maintains symbolic balance, allowing mathematicians to scale equations without distorting their truth.
How the Property Reinforces Logical Consistency in Algebra
At its core, the multiplication property ensures that transformations applied uniformly to an equation remain valid. Consider the equation \( 3 = 3 \)—a trivial truth.
When both sides are multiplied by 5:
3 × 5 = 3 × 5
≠
15 = 15
The equality endures. This conservation of truth supports algebraic manipulation, enabling steps that simplify complex expressions while preserving validity.
For more complex equations, such as \( x + 7 = 2x - 3 \), the same principle applies. Multiplying both sides by a non-zero constant isolates variables cleanly:
(x + 7) × c = (2x - 3) × c
Applying multiplication preserves structure.
Dividing both sides by the same value afterward yields consistent solutions, safeguarding mathematical integrity.
Scaling Ratios and Proportional Reasoning
One of the most intuitive applications lies in ratio equality: if \( \frac{a}{b} = \frac{c}{d} \), multiplying numerator and denominator by a common factor scales both parts equally, maintaining proportionality. This forms the bedrock of proportional reasoning in science, economics, and even cooking. For instance, a recipe scaled from 4 to 6 servings uses multiplication to adjust all ingredients evenly—without losing the original ratio.
Physicists leverage this property to maintain physical consistency.
When balancing equations of motion or energy conservation laws,


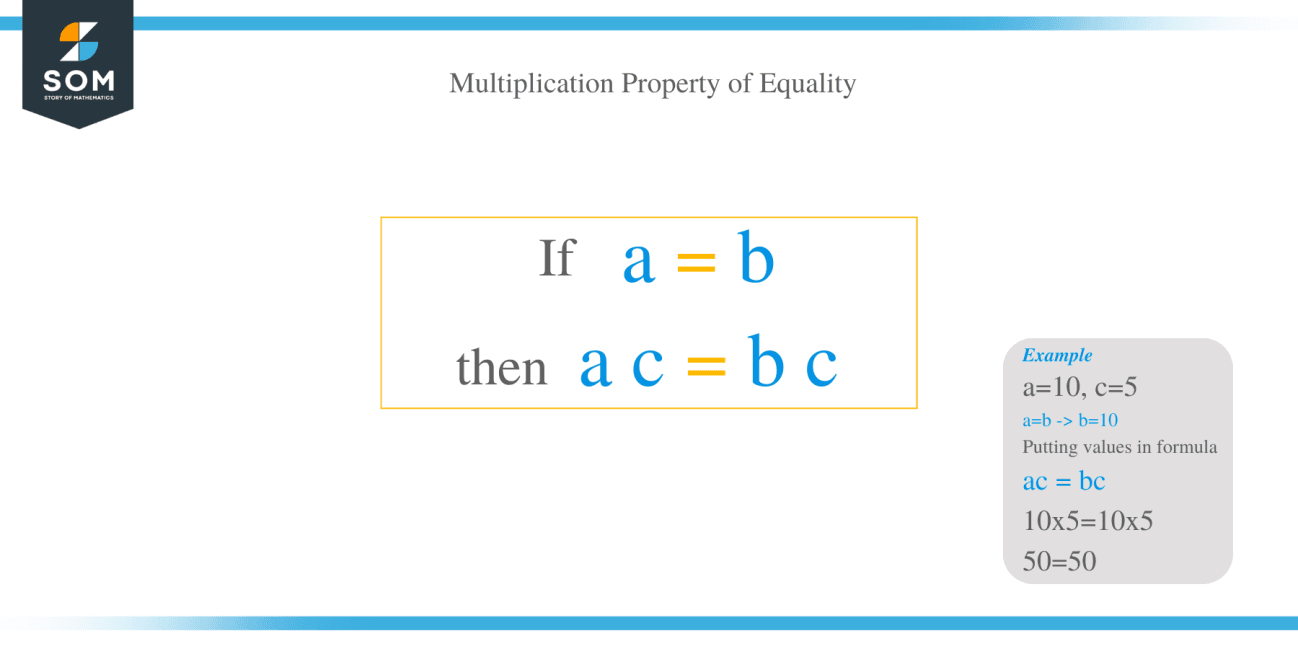
Related Post
Tal Fishman Net Worth and Earnings

Fixing the Silence: How Cyberpunk 2077 Dragged Players into Voice-Free Nightmares

The Face of Justice in Action: Inside the Belmont County Jail Roster
Disclosing Jess Brolin: One Deep Dive

