How to Find the Y-Intercept Using Two Points: A Step-by-Step Guide
How to Find the Y-Intercept Using Two Points: A Step-by-Step Guide
Determining the y-intercept from two given points is a foundational skill in coordinate geometry, essential for graphing linear equations and analyzing real-world data. Whether you're a student mastering linear functions or a professional translating data into visual insight, knowing how to calculate the y-intercept from two points offers clarity and precision. This method relies on the fundamental principle that a straight line is uniquely defined by its slope and one data point—making it straightforward, even when visualizing equations feels complex.
Understanding the Basics: What Is the Y-Intercept?
The y-intercept marks the point at which a line crosses the y-axis, represented algebraically as (0, b), where *b* is the y-intercept value.It reveals where the line begins its vertical rise or fall, offering insight into the function’s behavior at the origin of the vertical coordinate. In practical terms, the y-intercept helps answer critical questions—such as initial value in financial models or baseline measurements in scientific data. Because this point anchors the entire line on the y-axis, identifying it correctly enables accurate plotting and equation construction.
The Power of Two Points: Why Two Known Coordinates Are Enough
When given two distinct points on a straight line, two data points, the problem becomes solvable without relying on slope assumptions or guesswork. Each point provides a pair of coordinates (x, y) that must satisfy the linear equation: y = mx + b. By substituting these values into the equation, one equation is formed per point, allowing simultaneous solution to find both slope and intercept.As mathematician William Stringfellow once observed, “A line with two points defines everything—slope, intercept, and trajectory—no extra assumptions needed.” This principle forms the basis of a reliable, repeatable method used in both classroom learning and real-world data analysis.
Step-by-Step: Finding the Y-Intercept with Two Points
Begin by clearly identifying the two known points: let (x₁, y₁) and (x₂, y₂) represent the connections on the line. For example, consider the points (2, 5) and (−1, −4).The first step is to compute the slope *m* using the formula: m = (y₂ − y₁) / (x₂ − x₁). Substituting values: m = (−4 − 5) / (−1 − 2) = (−9) / (−3) = 3. With the slope determined, the next move is to substitute one point and the computed slope into the slope-intercept form, y = mx + b.
Using the point (2, 5): 5 = 3(2) + b → 5 = 6 + b → b = 5 − 6 = −1. Thus, the y-intercept is −1, and the line crosses the y-axis at (0, −1). This clean substitution method ensures accuracy and avoids common calculation errors.
Another example: given (4, 10) and (−2, 2), compute slope m = (2 − 10) / (−2 − 4) = (−8)/(−6) = 4/3. Then using (4, 10): 10 = (4/3)(4) + b → 10 = 16/3 + b → b = 10 − 16/3 = (30 − 16)/3 = 14/3. The y-intercept here is 14/3 ≈ 4.67, demonstrating how fractions emerge naturally when working with non-integer coordinates.
Visualizing the Result: Plotting the Y-Intercept on Graphs
Accuracy in identifying the y-intercept enables precise plotting. Plot the point (0, b) on the graph: for the first example, (0, −1) lies on the y-axis, directly marking the vertical intercept. From this reference, draw the line using the slope: rising 3 units for every 1 unit right, extending the line until it crosses the y-axis.The intersection at (0, −1)
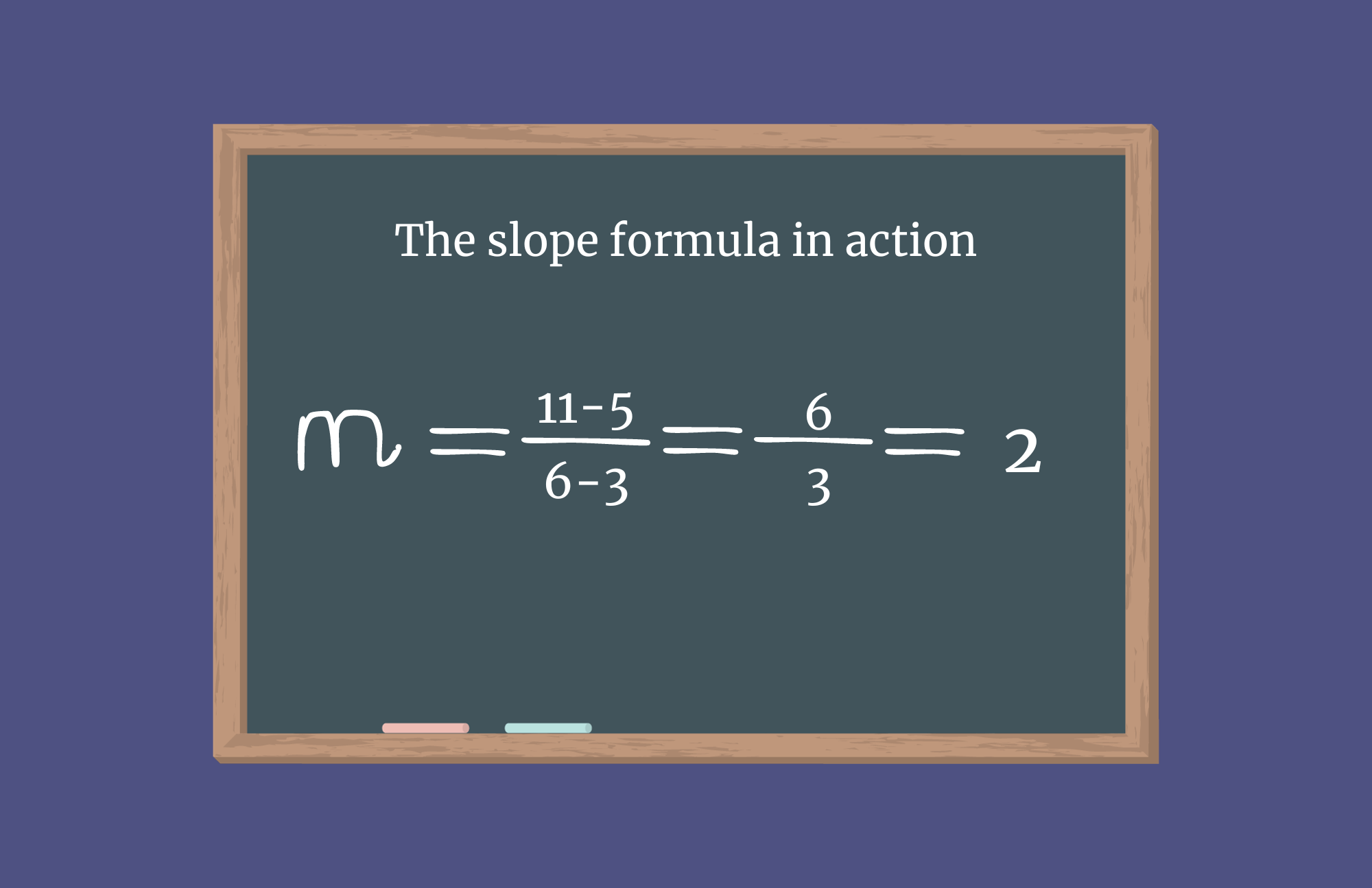



Related Post
Prince Nana Paid Ridiculous Amount for Uber to Reach ROH Event
Progressive Containment Structures: Examining the Xjail System for Supreme Safety
The Next Big Shift After Erome Mp4: A New Era in Digital Content, Content Creation, and Consumer Expectations

