How to Find the Y-Intercept: The Essential Step in Mastering Linear Equations

Understanding the y-intercept is a foundational skill in algebra—yet reaching it often draws confusion from students and learners alike. The y-intercept marks the point where a linear equation crosses the y-axis, revealing critical insights into a function’s behavior and its real-world implications. Whether analyzing slope, predicting values, or interpreting data, identifying this key coordinate is nonnegotiable.

This article unpacks the precise methods, Numerous tools, and practical examples that make locating the y-intercept transparent and efficient—no prior expertise required.

What Has the Y-Intercept Got to Do with Linear Equations?

The y-intercept is the y-coordinate of the point where a line intersects the vertical axis—mathematically represented as (0, b) in the slope-intercept form equation y = mx + b. Unlike slope, which explains steepness, the y-intercept pinpoints the vertical starting point, from which the entire line unfolds.

“Knowing where a line begins is as important as knowing how it rises,” notes Dr. Elena Martinez, math educator and curriculum specialist. “It’s the anchor that makes linear relationships interpretable.” Every linear equation reveals two core pieces of information: the slope (m), dictating change, and the y-intercept (b), defining the origin in vertical space.

This relationship ensures clarity across domains—from economics forecasting to physics modeling. Without knowing where y = 0 starts, predicting outcomes or drawing conclusions becomes significantly more speculative.

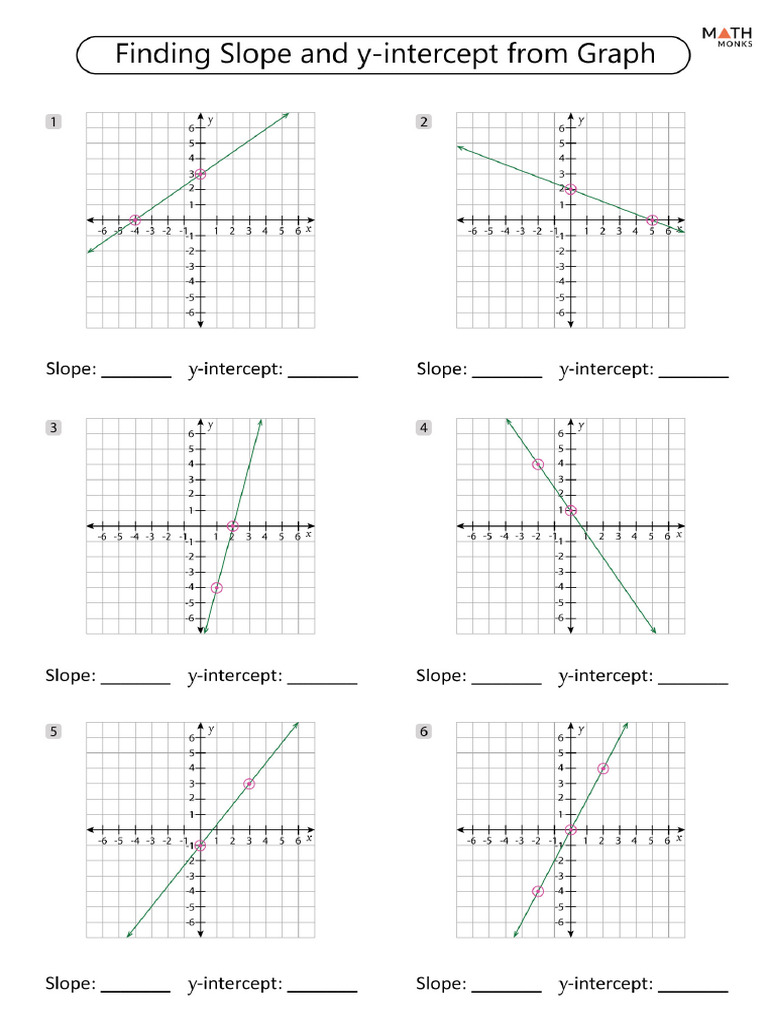
Step-by-Step Methods to Find the Y-Intercept

Finding the y-intercept is a straightforward process, but clarity lies in consistent application of key techniques.

Each method leverages the power of the slope-intercept form, y = mx + b, where b is the y-intercept by definition.

1. Direct Extraction in Slope-Intercept Form When an equation is explicitly written as y = mx + b, the y-intercept is immediately visible: b is the constant term. For example, in y = 3x – 6, b = –6, so the y-intercept is (0, –6).

   This method is fastest and most intuitive when available.

2. Substitution of Zero for x Substitute x = 0 directly into any linear equation: y = m(0) + b simplifies to y = b. This works for all forms—whether expressed as y = mx + b, Ax + By = C, or even real-world tabular data. Plugging x = 0 isolates b unambiguously.

   For instance, given y = –2x + 5, setting x = 0 yields y = 5, confirming the y-intercept at (0, 5).

3. Graphical Interpretation On a coordinate plane, locate where the line crosses the y-axis—location where x = 0. This visual method strengthens understanding, especially with graphing tools. Use graphing calculators or online platforms like Desmos to plot the line and visually confirm the intercept.

Each method reinforces the core principle: the y-intercept is the constant term in slope-intercept form, or the output when input is zero.

Consistency in approach eliminates confusion and builds mathematical fluency.

Real-World Examples That Bring the Y-Intercept to Life

To appreciate the y-intercept beyond abstract symbols, consider tangible applications. In finance, a linear revenue model might be R = 75x – 2000, where x is units sold and R is revenue in dollars.

Here, b = –2000 signals fixed pre-sales costs—the intercept reveals the break-even baseline. Understanding this helps businesses plan break-e