From Spheres to Streets: How Spherical Coordinates Transform 3D Space into Everyday Cartesian Mapping

For those navigating the intersection of abstract mathematics and real-world applications, the transformation from spherical coordinates to Cartesian coordinates is far from a mere academic exercise—it’s a foundational bridge enabling precise modeling across engineering, physics, computer graphics, and navigation. By converting angular positions and radial distances into precise x-y-z placements, this mathematical tool enables everything from GPS guidance to 3D rendering and robotic orientation. This transformation, though rooted in geometry, powerfully underpins technologies we rely on daily, shifting invisible spherical data into tangible Cartesian space with remarkable accuracy.

The Core Math: How Spherical to Cartesian Coordinates Work

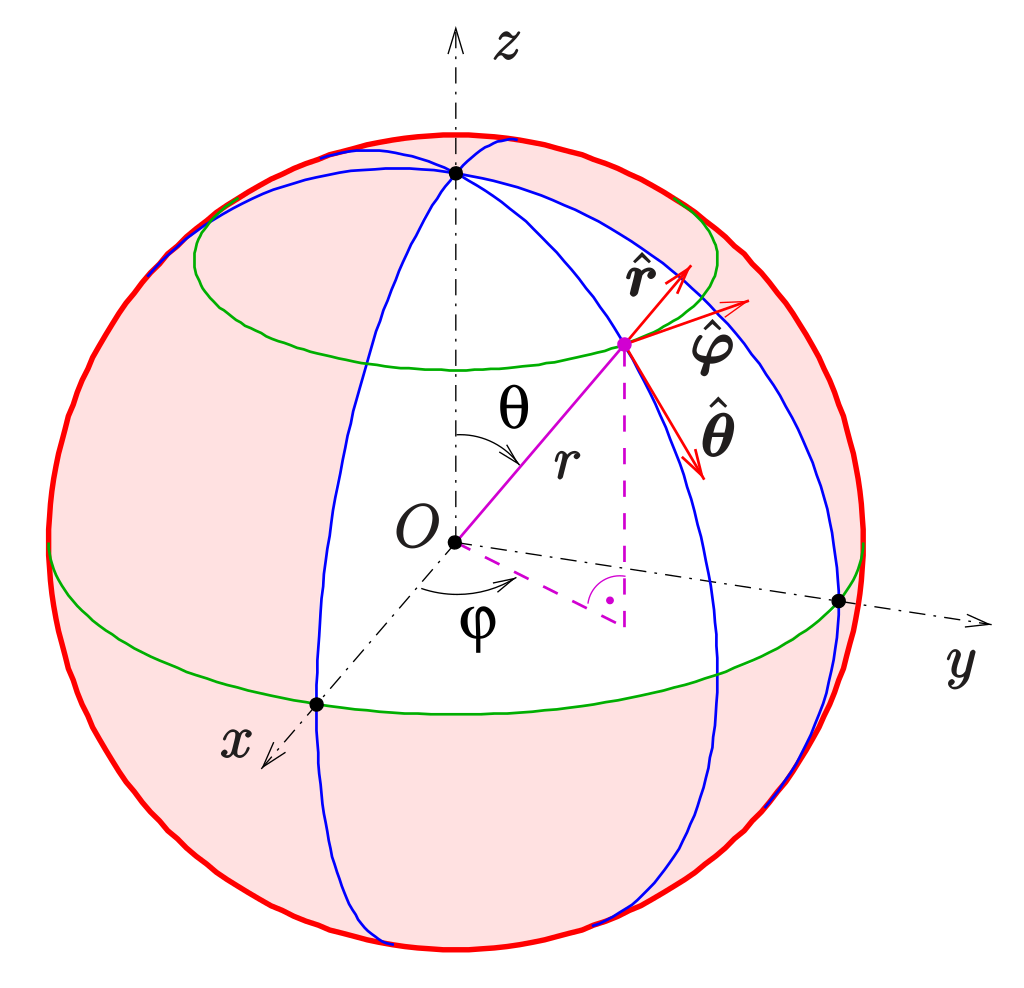
Spherical coordinates (ρ, θ, φ) define a point in space using three parameters: ρ—the radial distance from the origin, θ—the azimuthal angle in the xy-plane from the positive x-axis, and φ—the polar angle from the positive z-axis. The conversion to Cartesian coordinates (x, y, z) is mathematically elegant and geometrically intuitive: - x = ρ × sin(φ) × cos(θ) - y = ρ × sin(φ) × sin(θ) - z = ρ × cos(φ) These equations reflect the spatial logic of 3D Euclidean space—projection onto planes, scaling by radius, and angular deflection from reference axes. The sine and cosine components encode directional orientation, while ρ acts as the anchor point.

This precise mapping ensures no loss of spatial fidelity when switching representation, making spherical-to-Cartesian conversions indispensable for applications requiring exact positional data.

Understanding this conversion is critical when designing systems from drone navigation to medical imaging, where angular input must translate into exact location locations. Expert mathematician Dr.

Elena Torres notes: “The spherical-to-Cartesian transformation is not just a formula—it’s a lens that converts abstract angular awareness into concrete spatial reality.”

Key Components Explained

- **Radial Component (ρ):** Distance from the origin to the point; non-negative (ρ ≥ 0). - **Azimuth Angle (θ):** Angle in the x-y plane from the x-axis, measured clockwise; conventional range 0 ≤ θ < 2π radians. - **Polar Angle (φ):** Angle from the positive z-axis; typically 0 ≤ φ ≤ π radians, with φ = 0 pointing to the origin’s positive z-direction.

Each parameter contributes uniquely: ρ sets the "where," θ shifts left/right, and φ determines height from the horizontal plane. Together, they partition space into angular sectors and radial layers, forming a dense and continuous coordinate framework.

The Role of Spherical Coordinates in Modern Technology

Modern technology thrives on spatial data representation, and spherical coordinates serve as a pivotal intermediate step for systems relying on radial symmetry or angular precision.

For instance: - **GPS Navigation Systems:** Satellites transmit spherical position data (latitude, longitude, altitude), which users and algorithms convert to Cartesian coordinates for short-path routing algorithms. - **Computer Graphics and VR:** 3D rendering engines use spherical coordinates to animate celestial bodies, simulate light sources, or track user head orientation in immersive environments, then map those orientations into screen or virtual space coordinates. - **Robotics and Sensors:** LIDAR and ultrasonic sensors capture surrounding objects in spherical form; transforming this data into Cartesian coordinates allows robotic systems to map, avoid obstacles, and navigate complex environments.

- **Medical Imaging:** In ultrasound or CT scans, spherical sampling patterns are transformed into Cartesian (x-y) or Cartesian-volume representations for precise tumor localization and surgical planning. This conversion enables systems to leverage spherical symmetry—natural in many physical phenomena—while delivering location data in a universally understood Cartesian framework.

Mathematical Rigor and Computational Efficiency

At the heart of the spherical-to-Cartesian transformation lies a mathematical compactness that enhances both accuracy and computational performance.

Unlike Cartesian bounds defined by complex quadratic constraints, spherical coordinates decompose spatial relationships into clean, linear trigonometric functions. This decomposition reduces computational overhead in iterative algorithms, such as those used in ray tracing or finite element analysis. Moreover, the transformation supports robust interpolation and sampling in numerical simulations.

When modeling electromagnetic fields around a sphere or simulating wave propagation from a central point source, angular components captured in spherical coordinates yield smooth, continuous gradients when mapped to cartesian grids. This efficiency is critical in real-time applications, including autonomous drone swarms and augmented reality overlays.

Real-World Example: Navigating from Radius to Room Coordinates

Consider autonomous indoor robots delivering packages.

These systems detect surrounding landmarks—corners, doors, shelves—using angular sensors, stored as spherical data (distance and angle). To plot safe routes, coordinates must align with a floor plan in Cartesian space. The transformation enables: - Conversion of local angular observations into global x-y frame placements.

- Collision detection using precise grid-based rescaling. - Dynamic path recalculations as new spherical data arrives. This seamless translation ensures robots interpret angular cues—“turn 30 degrees clockwise at 2 meters”—into actionable x-y commands, blending perception with spatial logic.

The Transformation as a Spatial Language

Spherical coordinates and their Cartesian counterpart form a universal spatial language, bridging angular insight andCartesian precision. This conversion is not just computational—it’s interpretive, translating intuitive directional awareness into coordinates machines understand. Whether guiding a self-driving car through curved cities, rendering lifelike digital environments, or mapping the microstructure of materials, the spherical-to-Cartesian bridge enables clarity, accuracy, and innovation.

In a world increasingly driven by spatial intelligence, mastering this transformation empowers engineers, scientists, and developers to turn abstract angles into concrete locations, driving progress across technology and human experience. The true power of spherical coordinates to Cartesian conversion lies in its ability to make the abstract tangible—turning celestial observations and radial measurements into the precise spatial data that powers tomorrow’s spatial technologies.