Delta Symbol: The Mathematical Triangle Defining Space, Structure, and Strategy
Delta Symbol: The Mathematical Triangle Defining Space, Structure, and Strategy
In the intricate language of mathematics, few symbols carry as much geometric depth and interdisciplinary reach as the Delta symbol — denoted by the triangle: Δ. From geometry and calculus to engineering and strategic planning, Δ serves not only as a visual shorthand for change and transition but also as a foundational element in modeling dynamic systems. This article probes the multifaceted role of Δ, revealing how a simple triangular motif underpins advanced mathematical reasoning and real-world applications across disciplines.
At its core, the Delta symbol originates in ancient geometry, where the triangle represents stability, proportion, and transformation. The Greek letter Δ (Delta) encapsulates these qualities through its three equal sides and angled apex — a shape that, despite its simplicity, embodies powerful mathematical principles. In Euclidean geometry, Δ appears in foundational constructions: from the sum of interior angles equaling 180 degrees, to the Pythagorean theorem, Δ’s form serves as the basis for deriving relations between lengths and areas.
The symbol transcends mere representation — it signifies a measurable change, a shift in condition, or the emergence of new states.
Geometry and Calculus: Where Δ Shapes Mathematical Rigor
In mathematical pedagogy, the Delta symbol is indispensable. Geometers frequently invoke Δ to denote variables representing change — such as Δx (a small change in x) or Δt in time intervals — enabling precise formulations of rates and gradients. But the significance deepens in calculus, where Δ forms the conceptual bedrock of differentiation and integration.The finite-to-infinite transition is one of calculus’s central themes, and Δ plays a pivotal role in this evolution.
The Δx in the difference quotient — Δx = xₕ – xₘ — quantifies how infinitesimal changes accumulate into the derivative, Δx/Δt yielding velocity in kinematic equations. This ratio, grounded in Δ, becomes a bridge between discrete and continuous motion.
Similarly, in definite integration, Δ appears implicitly through the subdivision of intervals: approximating area under curves via rectangles relies on summing ΔA = f(x)Δx over subintervals, converging to the integral as Δx approaches zero. As physicist and author Richard Feynman once remarked, “The beauty of math is in how a single symbol like Δ can anchor both intuition and rigor.”
Δ in Linear Algebra and Systems Modeling
Beyond calculus, Δ emerges as a vital construct in linear algebra and systems theory.Matrices encoding transformations — rotations, scaling, shears — frequently feature Δ in their entries, signaling discrete shifts or preparatory changes. For instance, a transformation matrix may include Δ components to account for initial offsets or transitional states in models of evolution, economics, or signal processing.
In network theory, Δ aids in analyzing structural shifts: when edge weights or node connections change, these updates are described using ΔE or ΔC, enabling quantification of flow disruptions or connectivity evolution. Network resilience, a key metric in infrastructure planning, often depends on detecting and measuring Δ values across dynamic graphs.
In this digital age, where real-time data streams shape decisions, Δ symbols help codify change with mathematical precision—trans
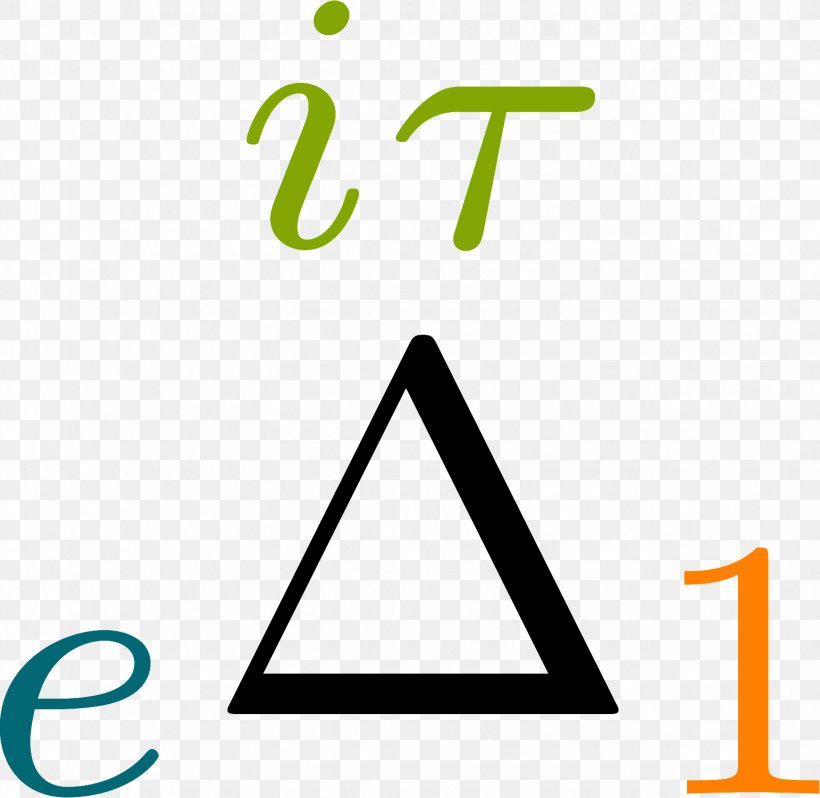


Related Post
Paul Dellegatto Fox 13 Bio Wiki Age Wife Brody Salary and Net Worth

What Is Nomor Rekening? The Vital Financial Lifeline in Indonesia’s Digital Ecosystem

From High School Grooves to Serious Racing: The Rise of Spicoli Fast Times at Ridgemont High
Michaela Watkins Actress Bio Wiki Age Height Family Saturday Night Live The Unicorn And Net Worth

